Simulating the ladybug clock puzzle

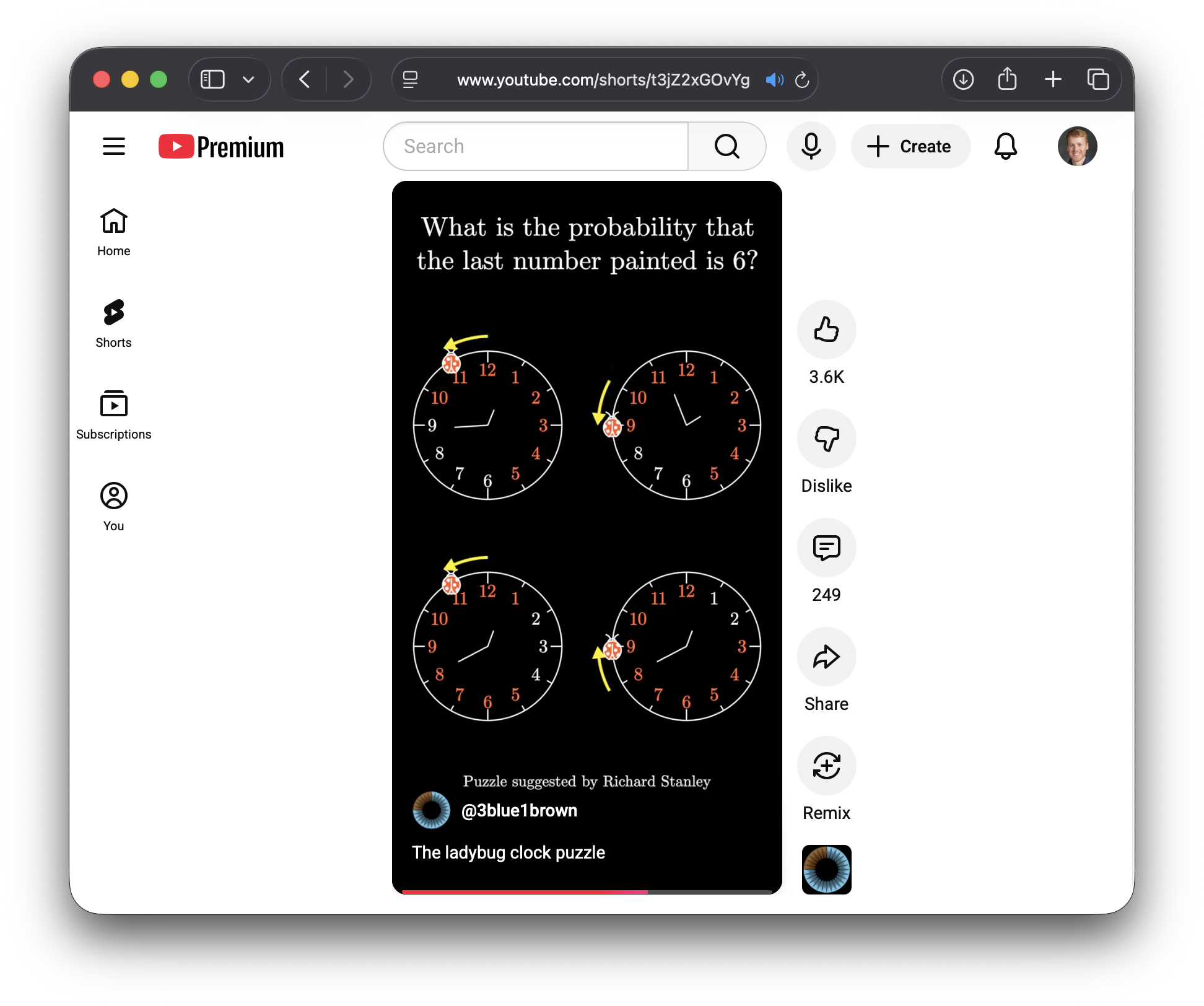
A few days ago, 3Blue1Brown posted a 60-second video describing a puzzle...

Imagine that a ladybug lands on the 12 o'clock marker of a clock. It then proceeds to move either clockwise or counterclockwise to the adjacent hour marker, one at a time, and repeats until all hour markers have been visited at least once.

What is the probability that it ends on the 6?

These sort of puzzles always intrigue me. They're simple to describe and at first might even look easy to solve, but as I dig into them, my intuition leads me astray.

What a fun Saturday morning project! I whipped up a simulator to try it out. It works like this:

    let position = 0; // 0-11 hour markers
    let visited = new Set([0]);

    while (visited.size < 12) {
        const direction = Math.random() < 0.5 ? -1 : 1;
        position = (position + direction + 12) % 12;
        visited.add(position);
    }

    return position;

See, it is simple. But before running the simulator, can you guess the probability of it ending on 6? What about 11 or 1? 3? The other numbers?

The simulator

Spoiler: Tell me the answer!

It stumped me. My guess was that 6 would be the most likely—it is the farthest away but it is also necessary to visit all other numbers first. The numbers closer to 12 would be gradually less likely. Am I right? It might remind you of other random walk problems.

So what is the answer? Well, I first ran the simulator 100 times and the results looked random. More runs! After ~1500 runs, all of the numbers were showing 8-10% likelihood with no discernable pattern. That isn't what I expected. After 5000 runs, they were all 8.4-9.7%. And then after 10,000 runs...

Based on the simulator, all numbers are equally likely with 9% probability, excluding 12 of course, since that is visited first and thus can't be last. The answer is ¹⁄₁₁.

An even more fun question? What is the average number of moves that the ladybug will make to visit all 12 numbers? I'd love to hear someone's explanation for that answer!